1. Melyik nem igaz az alábbi egyenlőtlenségek közül?
A
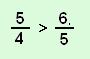
B
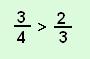
C
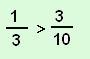
D
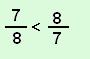
E
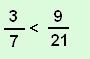
A | 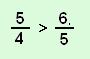 |
B | 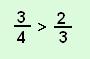 |
C | 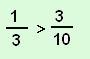 |
D | 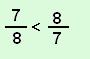 |
E | 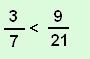 |
| A válasz betűjele: |
A |  |
B | 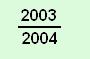 |
C | 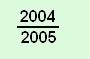 |
D | 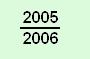 |
E | 1 |
| A válasz betűjele: |
A |
2006.03.15. |
B |
2006.03.20. |
C |
2006.03.25. |
D |
2006.03.26. |
E |
2006.03.30. |
| A válasz betűjele: |
 | 4. Az ábrán látható háromszögben az AD és CD szakaszok egyenlők. Mekkora a |
A | B | C | D | E |
| A válasz betűjele: |
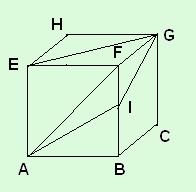 |
5. Az ábrán látható kocka felületén négy hangya versenyez, hogy melyikük ér hamarabb az Apontból a G pontba. A verseny tulajdonképpen szellemi, mert mindegyik ugyanolyan gyorsantud haladni,de az útvonalat megválaszthatják. Az erdei vöröshangya az AEG úton, a gyepihangya az AFG úton, a fáraóhangya az AIG úton (I a BF felezőpontja), a házi hangya azAz ABG úton halad. Melyikük ér először a G pontba? |
A |
Erdei vöröshangya |
B |
Gyepi hangya |
C |
Fáraóhangya |
D |
Házi hangya |
E |
Egyszerre érkeznek |
| A válasz betűjele: |
A |
Anti |
B |
Barni |
C |
Marci |
D |
Tomi |
E |
Nem lehet az adatokból meghatározni |
| A válasz betűjele: |
A |
12 |
B |
13 |
C |
14 |
D |
24 |
E |
25 |
| A válasz betűjele: |
 |
8. Hányadrésze a világos színű csillag területea nyolc egység oldalú négyzet területének? |
A |
|
B |
|
C |
|
D |
|
E |
|
| A válasz betűjele: |
A |
24 |
B |
28 |
C |
30 |
D |
32 |
E |
36 |
| A válasz betűjele: |
A |
0 |
B |
1 |
C |
2 |
D |
3 |
E |
több, mint három |
| A válasz betűjele: |