2. Mennyi a következő szorzás eredménye?
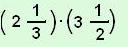
A
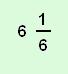
B
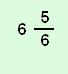
C
7
D
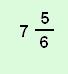
E
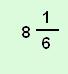
A | 8 |
B | 11 |
C | 13 |
D | 15 |
E | 18 |
| A válasz betűjele: |
A | 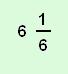 |
B | 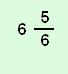 |
C | 7 |
D | 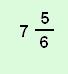 |
E | 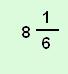 |
| A válasz betűjele: |
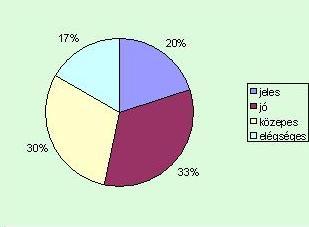 | 3. Az ábrán látható kördiagram egy matematikadolgozat eredményeinek |
A |
5 |
B |
6 |
C |
7 |
D |
8 |
E |
9 |
| A válasz betűjele: |
A | 16 |
B | 36 |
C | 56 |
D | 76 |
E | 96 |
| A válasz betűjele: |
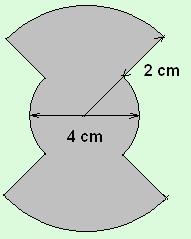 |
5. Hányszorosa az ábrán látható alakzat területe egy 2 cm sugarú kör területének?(Az alakzatot negyedkörívek és egyenes szakaszok határolják, a méretek az ábráról leolvahatók.) |
A |
2 |
B |
2,5 |
C |
3 |
D |
3,5 |
E |
4 |
| A válasz betűjele: |
A |
650 |
B |
653 |
C |
656 |
D |
660 |
E |
663 |
| A válasz betűjele: |
A |
13 |
B |
14 |
C |
15 |
D |
16 |
E |
17 |
| A válasz betűjele: |
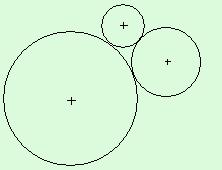 |
8. Három kör, melyek sugarai 1 cm, 2 cm és 3 cm, úgy helyezkednek el a síkon,hogy páronként érintik egymást. Hány négyzetcentiméter a középpontjaik általmeghatározott háromszög területe? |
A |
6 |
B |
6,5 |
C |
7 |
D |
7,5 |
E |
8 |
| A válasz betűjele: |
A |
264 |
B |
352 |
C |
364 |
D |
1320 |
E |
1584 |
| A válasz betűjele: |
A |
2 |
B |
4 |
C |
6 |
D |
8 |
E |
10 |
| A válasz betűjele: |