A | 4 |
B | 3 |
C | 2 |
D | 1 |
E | 0 |
| A válasz betűjele: |
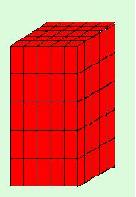
 | 2. Egy fából készült négyzetes oszlopot - melynek élei 5 cm, 5 cm és 10 cm - pirosra festettek,majd lapjaival párhuzamos síkokkal 1 cm x 1 cm x 2 cm -es kis négyzetes oszlopokra darabolták szét.Hány kis oszlopnak lesz pontosan egy lapja piros? |
A | 54 |
B | 64 |
C | 81 |
D | 98 |
E | 125 |
| A válasz betűjele: |
3. Mennyi a következő szorzat értéke? | |
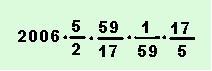 |
A | 1 |
B | 34 |
C | 118 |
D | 1003 |
E | 2006 |
| A válasz betűjele: |
A | 470 |
B | 474 |
C | 478 |
D | 480 |
E | 484 |
| A válasz betűjele: |
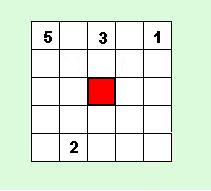 | 5. Az ábrán látható négyzetet úgy kell kitölteni az 1; 2; 3; 4; és 5számjegyekkel, hogy mindegyik sorban, mindegyik oszlopban ésa két átlóban is mindegyik számjegy pontosan egyszer szerepeljen.Milyen számjegy kerül a pirossal jelölt helyre? |
A | 1 |
B | 2 |
C | 3 |
D | 4 |
E | 5 |
| A válasz betűjele: |
A | 1 |
B | 2 |
C | 3 |
D | 4 |
E | Az előzőektől különböző |
| A válasz betűjele: |
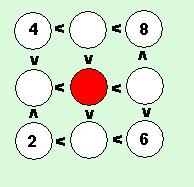 | 7. Az ábrába beírtuk 1-től kilencig a páros számokat.Ha beírjuk az - egyenlőtlenségeknek megfelelően - a páratlan számokat (1-től 9-ig)az üresen maradt helyekre, akkor milyen szám kerül a szinessel jelölt középső mezőbe? |
A | 1 |
B | 3 |
C | 5 |
D | 7 |
E | 9 |
| A válasz betűjele: |
A | 11 |
B | 12 |
C | 12,5 |
D | 13 |
E | 14 |
| A válasz betűjele: |
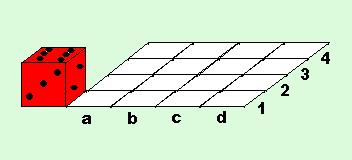
9. Az ábrán látható kocka rágördülve az a1 mezőre 5 pontot mutat.Továbbgördülve mekkora nem lehet a dobás értéke a c3 mezőn? |
A | 1 |
B | 2 |
C | 3 |
D | 4 |
E | 5 |
| A válasz betűjele: |
A | 18 |
B | 27 |
C | 52 |
D | 54 |
E | 108 |
| A válasz betűjele: |